PxMAF-X学习

本篇较为复杂，笔者也是边学边写，所以可能不能形成总体—>细节拆分的布局，只能先暂时是分点—>总结的学习步骤

瓶颈块

class Bottleneck(nn.Module):
    expansion = 4 # 输出通道数是中间通道数的4倍
    def __init__(self, inplanes, planes, stride=1, downsample=None):
        # inplanes:输入通道数
        # planes:压缩过后的中间层通道数
        # stride:步长，控制特征图尺寸
        # downsample:下采样（当输入和输出尺寸不匹配时使用）
        super(Bottleneck, self).__init__()
        # 1x1卷积:压缩
        self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        # 3x3卷积:处理
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride,
                               padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(planes)
        # 1x1卷积:解压
        self.conv3 = nn.Conv2d(planes, planes * 4, kernel_size=1, bias=False)
        self.bn3 = nn.BatchNorm2d(planes * 4)
        self.relu = nn.ReLU(inplace=True)# 激活函数
        self.downsample = downsample
        self.stride = stride

	def forward(self, x):
   		residual = x  # 保存原始输入（捷径）

    	# 主路径：三层卷积
    	out = self.conv1(x)
    	out = self.bn1(out)
    	out = self.relu(out)

    	out = self.conv2(out)
    	out = self.bn2(out)
    	out = self.relu(out)

    	out = self.conv3(out)
    	out = self.bn3(out)

    	# 如果需要下采样（输入和输出尺寸不匹配），对原始输入也做下采样
    	if self.downsample is not None:
    	    residual = self.downsample(x)

    	out += residual  # 主路径输出+原始输入（残差连接）
    	out = self.relu(out)  # 最后再通过激活函数

    	return out

这段定义了一个类定义的是ResNet中的瓶颈块，ResNet是残差网络，其主要的作用就是在神经网络传递的过程中解决退化问题，神经网络在不断的传递过程中，信息会存在偏差或缺失，这就导致深层次的神经网络可能会比浅层次的网络效果更差，而ResNet就是为了解决这个问题，主要得解决办法就是“抄近路”，每几层就加上一条“捷径”，让信息跳过中间层直接传递，这样就保证了信息不会丢失，而其中的基本单元就是残差块，残差快包括两个部分，分别是主路径和捷径，而我们这边定义的瓶颈块就是一种特殊的残差块，它是通过三个卷积层的组合，来完成一个压缩 - 处理 - 解压的过程。我在代码上加了一些注释，应该可以帮助理解。

举一个实例，就是这个样子

假设输入是256通道的特征图，中间层通道数设为64：

压缩阶段（1x1 卷积）：

输入：256 通道 → conv1 → 64 通道

减少了 3/4 的通道数，降低计算量
处理阶段（3x3 卷积）：

64 通道 → conv2 → 64 通道

保持通道数不变，专注提取特征
解压阶段（1x1 卷积）：

64 通道 → conv3 → 256 通道（恢复原始通道数）
残差连接：

将原始输入（256 通道）直接加到处理后的输出上

公式：最终输出 = 卷积处理结果 + 原始输入

Conv2d函数的意思

代码中有这样一行：

1	`nn.Conv2d(inplanes, planes, kernel_size=1, bias=False)`

Conv2d是什么呢？这行代码表示的是一个1x1卷积层，它在这里负责两件事，第一个是把高通道数压成低通道数，第二个是再把低通道数恢复到高通道数，我们用最通俗的话来说，就是如果你是一个乐队演奏家，要调整现在的乐器的音量：你原先有10个乐器（通道）同时演奏，现在你对它们进行1x1卷积，给每个乐器提供一个“音量调整系数”，在调整后，就可以只用保持5个乐器的声音（通道数减少），或者达到20个乐器的效果（通道数增加）

BatchNorm2d函数的意思

还有这样的一行代码：

1	`self.bn1 = nn.BatchNorm2d(planes)`

BatchNorm2d又是什么呢？这里是使用了PyTorch创建了一个二维批量归一化层（Batch Normalization），简称BN 层，这个看起来抽象难以理解，实际上它做了两件事，归一化和缩放与平移，首先，对当前批次（Batch）中的所有样本，计算每个通道的均值和方差。然后，用公式：$(x - 均值) / \sqrt(方差 + \epsilon)$，其中$ $是一个很小的数（如 1e-5），防止除零错误（基本操作）。最后，使用两个可学习的参数：

γ（缩放因子）：控制数据的缩放程度

β（平移因子）：控制数据的平移程度

公式：γ * 归一化后的数据 + β

这里需要指出的是，在上面的归一化公式计算过后，数据的结果会变成均值0，方差1（有兴趣的可以推导一下）

这里举一个非常通俗易懂的例子来解释BN层的作用：

如果你是大学里面的一个老师，你教的班很多同学都要挂科了，为了你们班上的及格率，你使出了你的“捞人大法”，先用$(x - 均值) / \sqrt(方差 + \epsilon)$将分数变为平均分0，标准差为1的一串数，然后你开始设置你的γ和β值，如果你想平均分为70，那么你就将β调整为70，如果你分数差距能够大一些，那么就将γ设置得更大一些，比如1.5

RELU函数的意思

1	`self.relu = nn.ReLU(inplace=True)`

RELU是什么意思？简单来说，ReLU 把所有负数变成 0，正数保持不变，就是一个非常简单的函数，但是它具有什么样的意义呢？两个意义：一个是引入非线性，激活函数显而易见是非线性函数，如果没有激活函数，无论神经网络有多少层，最终都等价于一个线性函数（因为线性变换的组合还是线性的）第二个，在一定程度上能够解决梯度的消失问题（这块我也没有太搞懂，查的资料上是这么讲的），这里的梯度其实就是高数里面梯度概念的衍生，梯度是用来指示神经网络应该朝哪个方向去调整的，并且调整多少。

骨干网络

class ResNetBackbone(nn.Module):
    def __init__(self, block, layers, in_channels=3):
        self.inplanes = 64
        super(ResNetBackbone, self).__init__()
        # 通过7x7卷积+BN+ReLU+最大池化，快速缩小特征图尺寸（降维）
        self.conv1 = nn.Conv2d(in_channels, 64, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(64)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        # layer1：通道数 64，特征图尺寸不变
        # layer2：通道数 128，特征图尺寸减半（stride=2）
    	# layer3：通道数 256，特征图尺寸减半
        # layer4：通道数 512，特征图尺寸减半
        self.layer1 = self._make_layer(block, 64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2)
		# 随着层数加深，通道数增加，特征图尺寸减小，抓住更多特征，抽离出更多关键信息
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
            elif isinstance(m, nn.BatchNorm2d):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)

    def _make_layer(self, block, planes, blocks, stride=1):
        downsample = None
        if stride != 1 or self.inplanes != planes * block.expansion:
            downsample = nn.Sequential(
                nn.Conv2d(self.inplanes, planes * block.expansion,
                          kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(planes * block.expansion),
            )

        layers = []
        layers.append(block(self.inplanes, planes, stride, downsample))
        self.inplanes = planes * block.expansion
        for i in range(1, blocks):
            layers.append(block(self.inplanes, planes))

        return nn.Sequential(*layers)

    def forward(self, x):
        # 通过第一个卷积层和池化层，得到初始特征
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)
	    # 逐层提取特征，每层输出的特征图尺寸逐渐减小，通道数逐渐增加
        x1 = self.layer1(x)
        x2 = self.layer2(x1)
        x3 = self.layer3(x2)
        x4 = self.layer4(x3)
	   # 返回四层的特征图，用于后续任务
        return [x1, x2, x3, x4]

这一块是ResNet的核心部分，前面和后面基本上跟上一段还是很像的，我加了一些注释，应该没有问题，难点应该是在19-41行之间，但是在这之前，我们先补一个小点，就是maxpool函数的意思

maxpool函数的意思

1	`self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)`

这个函数也是PyTorch里面的，意思为最大池化层，最大池化就像一个 “筛选器”，它在输入数据上滑动一个小窗口，每次只保留窗口内的最大值，其他值全部丢弃。我们的kernel_size就是池化窗口的大小（单位也是像素），stride是每次走的步长（单位是像素），padding在输入数据周围填充多少圈 0（这里是1圈）

我们在进行池化后，提取出了图像中最为主要的特征，并且减小了数据尺寸

Kaiming 初始化方法

1	`nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')`

Kaiming初始化是专门为ReLU激活函数设计的初始化方法，它的目标是：让神经网络各层的激活值和梯度的方差在传播过程中保持稳定，避免出现梯度消失或爆炸。

这里讲的有些抽象了，我们先来解决一下里面的参数的意义：

m.weight：需要初始化的卷积层权重张量。

mode='fan_out'：

控制权重初始化的缩放因子。
'fan_out'保持输出方差的稳定性（更适合卷积层）。

nonlinearity='relu'：

指定激活函数类型为 ReLU。
Kaiming 初始化会根据不同的激活函数调整缩放因子（ReLU舍弃掉了负的一半区间，ReLU 需要额外除以 2）。

初始化的结果是，让权重服从正态分布，标准差为$\sqrt(\frac{2}{fanout})$，fan_out 表示输出通道数，控制方差以保持梯度稳定。

如果觉得这个表述还是太抽象的话，举个最简单的例子：如果组织一场接力赛，如果我们每个选手的初始跑步速度都是随机的，那么可能会出现几个问题，前面的选手跑得太快，后面的选手接不住棒（梯度爆炸），前面的选手跑得太慢，接力棒到后面几乎停了（梯度消失），而我们的Kaiming初始化就是根据赛道长度和选手数量，精确计算每个选手的初始速度，确保接力棒能稳定、快速地传递到终点。

这个初始化方法基本上就是对照着ReLU激活来的，也是特别适合ResNet这种大量使用ReLU的网络。

那么我们终于可以开始解释了

参数初始化操作

for m in self.modules():# 遍历模型中的每一个层（包括卷积层、BN层、ReLU等）
	if isinstance(m, nn.Conv2d):
		nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
	elif isinstance(m, nn.BatchNorm2d):
		nn.init.constant_(m.weight, 1)
		nn.init.constant_(m.bias, 0)

前置的东西讲完，这个东西就很好解释了，这段代码就是神经网络里面的参数初始化操作，它会遍历模型里面的每一个层，并且根据层的类型设置不同的初始值，如果是卷积层，那么就使用Kaiming初始化，如果是BN层，就使用BatchNorm 层初始化（前文都有介绍）。其实，这些初始化，都是为了保证梯度在神经网络中传递的稳定性

_make_layer函数

def _make_layer(self, block, planes, blocks, stride=1):
    # block: 残差块类型（如Bottleneck）
    # planes: 基础通道数（如64、128等）
    # blocks: 该层包含的残差块数量
    # stride: 步长，控制特征图尺寸是否减半（默认为1）
    downsample = None
    if stride != 1 or self.inplanes != planes * block.expansion:
        downsample = nn.Sequential(
            nn.Conv2d(self.inplanes, planes * block.expansion,
                      kernel_size=1, stride=stride, bias=False),
            nn.BatchNorm2d(planes * block.expansion),
        )

    layers = []
    layers.append(block(self.inplanes, planes, stride, downsample))
    self.inplanes = planes * block.expansion
    for i in range(1, blocks):
        layers.append(block(self.inplanes, planes))

    return nn.Sequential(*layers)

我把参数的意义写在备注上，接下来就是解释了，这一段是定义ResNet中的“残差层”的核心逻辑，就是通过堆叠多个残差块来组成网络的一层，这是一个大层，而这个大层的特点就是第一层可能包括下采样（downsample）操作，用于调整特征图的尺寸和通道数，后续层保持相同的通道数和特征图尺寸，这里我再解释一下什么是下采样，下采样可以简单的理解为“缩小图片”的操作，目的是让图片变小同时保留重要信息，至于下采样的方式，就是可以用之前的“池化层”，每隔两个像素来取一个最大值，图片直接编程之前的一半，或者使用1x1的卷积层，通过调整步长，比如stride=2，让输出的图片尺寸缩小。

而我们这边需要判断是否要进行下采样，主要是有两种情况：

stride != 1：需要调整特征图尺寸（通常为 2，即减半）

self.inplanes != planes * block.expansion：输入通道数与输出通道数不匹配

这边下采样的实现就是用1x1卷积来调整通道参数

下采样结束之后，其实后续就没什么特殊的了，就是保持相同的通道数和特征图尺寸，输入通道数已经在第一层后更新为planes * block.expansion了

假设我们要构建 ResNet 的第二层（layer2）：

block = Bottleneck（瓶颈块，expansion=4）
planes = 128
blocks = 4（该层有 4 个瓶颈块）
stride = 2（需要下采样，特征图尺寸减半）

第一个瓶颈块： - 输入通道数：256（来自 layer1 的输出） - 中间通道数：128 - 输出通道数：128×4 = 512 - 包含下采样：1x1 卷积（256→512，stride=2） - 特征图尺寸：从 56x56→28x28

后续三个瓶颈块： - 输入 / 输出通道数：512→512 - 中间通道数：128 - 特征图尺寸保持 28x28 不变

这样子基本上我们的骨干网络就全部讲清楚了，可以不断地往下传。

特征金字塔网络

class FeaturePyramidNetwork(nn.Module):
    def __init__(self, in_channels_list, out_channels):
        super(FeaturePyramidNetwork, self).__init__()
        self.inner_blocks = nn.ModuleList()
        self.layer_blocks = nn.ModuleList()
        for in_channels in in_channels_list:
            if in_channels == 0:
                continue
            # 1x1 卷积，用于调整不同层级特征的通道数（统一为out_channels）
            inner_block = nn.Conv2d(in_channels, out_channels, 1)
            # 3x3 卷积，用于处理融合后的特征
            layer_block = nn.Conv2d(out_channels, out_channels, 3, padding=1)
            self.inner_blocks.append(inner_block)
            self.layer_blocks.append(layer_block)
			# 这里还是对每一层进行BN初始化
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_uniform_(m.weight, a=1)
                nn.init.constant_(m.bias, 0)

    def forward(self, x):
        last_inner = self.inner_blocks[-1](x[-1])
        results = []
        results.append(self.layer_blocks[-1](last_inner))
        
        for i in range(len(x) - 2, -1, -1):
            inner_lateral = self.inner_blocks[i](x[i])
            feat_shape = inner_lateral.shape[-2:]
            last_inner = F.interpolate(last_inner, size=feat_shape, mode="nearest")
            last_inner = last_inner + inner_lateral
            results.insert(0, self.layer_blocks[i](last_inner))

        return results

在上面一个篇章，我们已经处理好了很多个大层，这里面的特征金字塔网络（Feature Pyramid Network, FPN），目标是融合不同层级的特征，就是把我们刚刚得到的诸多大层的特征再次融合在一起，使得我们的提取结果既有高度概括的特征，又有细致的细节，就是相当于“显微镜+望远镜”，既能看清细节，又能把握全局

前半部分的初始化过程我就不多说了，跟前面的内容有很多重合的，后面的forward函数还是有些意思的

def forward(self, x):
    # 处理最深层特征（最高语义，最小尺寸）
    last_inner = self.inner_blocks[-1](x[-1])
    results = [self.layer_blocks[-1](last_inner)]
    # 自顶向下融合过程
    for i in range(len(x) - 2, -1, -1):
        # 获取当前层特征并调整通道
        inner_lateral = self.inner_blocks[i](x[i])
        # 上采样高层特征，使其与当前层尺寸匹配
        last_inner = F.interpolate(last_inner, size=inner_lateral.shape[-2:], mode="nearest")
        # 特征融合：将上采样后的高层特征与当前层特征相加
        last_inner = last_inner + inner_lateral
        # 处理融合后的特征并保存结果
        results.insert(0, self.layer_blocks[i](last_inner))
    return results

我本来还是想继续写一些东西的，后来觉得代码注释已经把我想写的全部写完了，可能还是会觉得抽象，来举个例子吧：

假设输入是来自ResNet的四层特征:

C2: 256通道, 尺寸56×56（最浅层）

C3: 512通道, 尺寸28×28

C4: 1024通道, 尺寸14×14

C5: 2048通道, 尺寸7×7（最深层）

用 1x1 卷积将 C2→256，C3→256，C4→256，C5→256（假设out_channels=256）

自顶向下融合：

P5 = 调整后的C5（尺寸7×7）

P4 = 调整后的C4 + 上采样(P5)（尺寸14×14）

P3 = 调整后的C3 + 上采样(P4)（尺寸28×28）

P2 = 调整后的C2 + 上采样(P3)（尺寸56×56）

最终输出：

[P2, P3, P4, P5]（通道数均为256，尺寸从大到小）

大尺寸特征图（如 P2）适合检测小物体（保留了细节）

小尺寸特征图（如 P5）适合检测大物体（包含了高层语义）

基本上我们这个FPN也讲清楚了

多尺度注意力特征

class MAF_Extractor(nn.Module):
    def __init__(self, feat_dim=2048, maf_dim=256):
        super(MAF_Extractor, self).__init__()
        self.global_avgpool = nn.AdaptiveAvgPool2d((1, 1))# 全局平均池化
        self.fc = nn.Linear(feat_dim, maf_dim)# 全连接层，降维
        self.bn = nn.BatchNorm1d(maf_dim)# 批量归一化
        self.relu = nn.ReLU(inplace=True)# 激活函数

    def forward(self, x):
        x = self.global_avgpool(x)# 压缩特征图为1×1
        x = torch.flatten(x, 1)# 展平为一维向量
        x = self.fc(x)# 降维：feat_dim → maf_dim
        x = self.bn(x)# 归一化
        x = self.relu(x)# 激活函数
        return x

这段定义了一个MAF_Extractor（Multi-scale Attention Feature, MAF）的神经网络模块，如果简单解释MAF_Extractor 就像一个 “特征压缩器”，它接收高维的图像特征（例如 ResNet 输出的 2048 维特征），通过一系列操作将其转换为低维但更有代表性的特征（例如 256 维）。

里面的函数也非常好理解，很多是之前已经出现过的

AdaptiveAvgPool2d函数

1	`self.global_avgpool = nn.AdaptiveAvgPool2d((1, 1))`

假设输入是一个C×H×W的特征图（C 是通道数，H 和 W 是高度和宽度），全局平均池化会：

对每个通道（channel）单独处理
计算每个通道上所有像素值的平均值
输出一个C×1×1的向量，每个值对应一个通道的平均值

这个简单到不需要举例子了

参数就是矩阵的大小，因为这里输入的是(1,1)，如果两个参数都设成2，那么就会使2x2的矩阵

Linear函数

1	`self.fc = nn.Linear(feat_dim, maf_dim)`

全连接层就像一个 “翻译器”，把输入的特征向量（比如 2048 维）“翻译” 成另一个维度的向量（比如 256 维）。这个过程可以用一个线性方程表示：

y = Wx + b

x 是输入向量（维度：feat_dim）

W 是权重矩阵（维度：maf_dim × feat_dim）

b 是偏置向量（维度：maf_dim）

y 是输出向量（维度：maf_dim）

全连接层的参数就是W和b，这个数值需要通过训练来得到

feat_dim：输入特征的维度（这里是2048，来自上一层的输出）

maf_dim：输出特征的维度（这里是256，压缩后的特征维度）

我们需要特别注意的是，这个函数既可以用来降维，也可以用来升维，后面会多次遇到

姿势回归器

class PoseRegressor(nn.Module):
    def __init__(self, feat_dim=256, output_dim=24*3*3):
        super(PoseRegressor, self).__init__()
        self.fc1 = nn.Linear(feat_dim, 1024)# 第一个全连接层：升维
        self.dropout1 = nn.Dropout(0.5)# 第一个Dropout层
        self.fc2 = nn.Linear(1024, 1024)# 第二个全连接层
        self.dropout2 = nn.Dropout(0.5)# 第二个Dropout层
        self.fc3 = nn.Linear(1024, output_dim)# 第三个全连接层：输出结果
        self.relu = nn.ReLU(inplace=True)# ReLU激活函数

    def forward(self, x):
        x = self.dropout1(self.relu(self.fc1(x)))# 第一层：全连接+激活+Dropout
        x = self.dropout2(self.relu(self.fc2(x)))# 第二层：全连接+激活+Dropout
        x = self.fc3(x)# 第三层：直接输出结果
        return x

这段代码定义了一个姿态回归器（PoseRegressor），它的作用是从输入特征中预测人体的 3D 姿态。姿态回归器就像一个 “姿势解码器”，它接收一个特征向量（MAF_Extractor 输出的 256 维特征），然后预测出人体各个关节的 3D 位置。

这里面的Dropout让我自己想肯定是想不到的，给的说法是随机丢掉50%的神经元，防止过拟合，这可能是在实践中发现存在错误后而进行的修正吧

它的特点就是逐步处理特征，从 256 维→1024 维→1024 维→216 维（216 = 24 x 3 x 3）这个数字代表的就是24个关节点，每个关节点用3*3的旋转矩阵来表示，就是SMPL的核心参量了

为什么要升维？从 256 维升到 1024 维，让模型有更多 “空间” 学习复杂的姿势特征但是可能也是意味着维数越多，拟合出来的就越精确吧，反正Linear函数里面的W和b都是训练出来的，只要给合适的数据就行。

形状回归器

class ShapeRegressor(nn.Module):
    def __init__(self, feat_dim=256, output_dim=10):
        super(ShapeRegressor, self).__init__()
        self.fc1 = nn.Linear(feat_dim, 1024)
        self.dropout1 = nn.Dropout(0.5)
        self.fc2 = nn.Linear(1024, 1024)
        self.dropout2 = nn.Dropout(0.5)
        self.fc3 = nn.Linear(1024, output_dim)
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        x = self.dropout1(self.relu(self.fc1(x)))
        x = self.dropout2(self.relu(self.fc2(x)))
        x = self.fc3(x)
        return x

这里面的代码几乎完全相同，唯一不同的是最终输出维度是10维，是是因为我们的形状参数就是10维的（后来更新到50维，但是现在开源的还是只有10维），还是那句话，Linear函数里面的W和b都是训练出来的，所以这个模板在姿态和形状上面都可以使用。

相机回归器

class CamRegressor(nn.Module):
    def __init__(self, feat_dim=256):
        super(CamRegressor, self).__init__()
        self.fc = nn.Linear(feat_dim, 3)# 全连接层：256维→3维
        nn.init.zeros_(self.fc.weight)# 权重初始化为0
        nn.init.ones_(self.fc.bias)# 偏置初始化为1
        nn.init.constant_(self.fc.bias[0], 0.9)# 第一个偏置设为0.9

    def forward(self, x):
        return self.fc(x)

这段代码更简单，就是从输入特征中与预测相机参数，还是那话，由于Linear函数的存在，初始值不必太在意，我们这边需要关注一下它的输出的三位向量分别代表什么意思

缩放因子（scale）：控制人体在图像中的大小，值越大，人体看起来越大（相机离人体越近）
水平平移（tx）：控制人体在图像中的水平位置
垂直平移（ty）：控制人体在图像中的垂直位置

这些参数可以将 3D 人体模型投影到 2D 图像平面上，使其与输入图像中的人体对齐。

PyMAF-X模型（核心）

class PyMAF_X(nn.Module):
    def __init__(self, pretrained=True):
        super(PyMAF_X, self).__init__()
        self.backbone = ResNetBackbone(Bottleneck, [3, 4, 6, 3])# 特征提取骨干网络
        self.fpn = FeaturePyramidNetwork([256, 512, 1024, 2048], 256)# 特征融合
        self.maf_extractor = MAF_Extractor(2048, 256)# 多尺度注意力特征提取
        self.pose_regressor = PoseRegressor(256, 24*3*3)# 姿态回归
        self.shape_regressor = ShapeRegressor(256, 10)# 形状回归
        self.cam_regressor = CamRegressor(256)# 相机参数回归

        if pretrained:
            self._load_pretrained_weights()

    def _load_pretrained_weights(self):
        resnet = resnet50(pretrained=True)
        backbone_state_dict = self.backbone.state_dict()
        resnet_state_dict = {k: v for k, v in resnet.state_dict().items() if k in backbone_state_dict}
        backbone_state_dict.update(resnet_state_dict)
        self.backbone.load_state_dict(backbone_state_dict)

    def forward(self, x):
        features = self.backbone(x)# 提取多尺度特征
        fpn_features = self.fpn(features)# 融合特征
        global_feat = self.maf_extractor(features[-1])# 提取全局特征
        
        pose = self.pose_regressor(global_feat)# 预测姿态
        shape = self.shape_regressor(global_feat)# 预测形状
        cam = self.cam_regressor(global_feat)# 预测相机参数
        
        return {
            'pose': pose,
            'shape': shape,
            'cam': cam
        }

铺垫了这么久，终于千呼万唤始出来了，除了其中的预训练权重，其他的基本上是所见即所得了。预训练就是将已经训练好的ResNet50加载下来，将这些知识迁移到PyMAF-X中，站在巨人的肩膀上，大大减少了运算量。

虽然非常简单，我还是想在这边做一个总结，我们的处理流程

输入图像 → ResNet骨干网络 → 特征金字塔融合 → 全局特征提取 →

→ 姿态回归器 → 姿态参数

→ 形状回归器 → 形状参数

→ 相机回归器 → 相机参数

SMPL的实现

SMPL（Skinned Multi-Person Linear Model）是一种裸体的（skinned），基于顶点（vertex-based）的人体三维模型，能够精确地表示人体的不同形状（shape）和姿态（pose）。

前置概念

在进入SMPL模型之前，需要先明确2个概念：

1.顶点（vertex）：小三角形，看作一个顶点（记为N，在人体中应该是有6890个）

2.骨骼点：关节点，姿态估计的关键点（记为K，是23个三维旋转向量）

理论推导

我们先来一些模型参数Φ = {T, W, S, J, P}，这些参数不是输入量，这些参数是通过训练得到的，我们的输入参数是$\vecβ,\vecθ,\vecθ^*$

我们来逐个解释其中的含义：

$\vecβ=[\vecβ_1,…,\vecβ_{∣β∣}]^T$：形状参数，我们上面已经通过2D单目图像得到了

$\vecθ=[\vecω^T_0,…,\vecω^T_K]^T$：姿态参数，w_k指关节k相对于运动树（kinematic tree）中的父关节点的旋转轴角度，ω_k ∈ R³，我们上面也已经得到了

W ∈ R^N × K：一组混合权重，BS/QBS混合权重矩阵，即关节点对顶点的影响权重 (第几个顶点受哪些关节点的影响且权重分别为多少)

$S=[S_1,…,S_{|\vecβ|}]∈R^{3N×|\vecβ|}$：由$\vecβ$带来的顶点位置修正

P = [P₁, …, P_k] ∈ R^3N × k：由θ⃗带来的顶点位置修正

$\overline T∈R^{3N}$：T姿态，作为平均模型，后面的修改都是建立在它的基础上的

J: 将rest vertices转换成rest joints的矩阵（获取T pose的关节点坐标的矩阵）[完成顶点到关节的转化]

对于SMPL模型来说，我们主要分为几个步骤：

1.将shape缩放

2.根据shape调整joint

3.调整胖瘦变形

4.确定姿势

5.给骨架包裹外衣，蒙皮

SMPL 10个shape的意义分别对应的是：

0 代表整个人体的胖瘦和大小，初始为0的情况下，正数变瘦小，负数变大胖（±5）

1 侧面压缩拉伸，正数压缩

2 正数变胖大

3 负数肚子变大很多，人体缩小

4 代表 chest、hip、abdomen的大小，初始为0的情况下，正数变大，负数变小（±5）

5 负数表示大肚子+整体变瘦

6 正数表示肚子变得特别大的情况下，其他部位非常瘦小

7 正数表示身体被纵向挤压

8 正数表示横向表胖

9 正数表示肩膀变宽

$M(\vecβ,\vecθ;Φ)=W(T_P(\vecβ,\vecθ),J(\vecβ),\vecθ,W)R^{∣\vecθ∣×∣\vecβ∣}↦R^{3N}$：将形状和位姿参数映射到顶点

$W(\overline T,J,\vecθ,W):R^{3N×3K×|\vecθ|×|W|}↦R^{3N}$:标准线性混合蒙皮.

$B_P(\vecθ):R^{|θ|}↦R^{3N}$：输入是一系列姿势参数向量，代表姿势的相关形变引发的顶点的修正

B_S(β⃗) : R^|β| ↦ R^3N：输入是一系列姿势参数向量，代表姿势的相关形变引发的顶点的修正

$J(\vecβ):R^{∣β∣}↦R^{3K}$: 一个预测K个关节位置的函数.

每个关节j绕轴的旋转角用罗德里格斯公式转换成旋转矩阵：

$exp(\vec ω_j)=I+\hat{\overline ω_j}sin(∥\vec ω_j∥)+\hat ω^2_jcos(∥\vecωj∥)$

其中，$\vecθ=[\vecω^T_0,…,\vecω^T_K]^T$，参数通过$|\vecθ|=3×23+3=72$定义

$\overline ω=\frac{\vecω}{|∣ω|∣}$:为旋转的单位轴，单位化了

$\hatω$：斜对称矩阵，通过三维向量$\overline ω$组成

I：3 × 3单位矩阵

下面就是这个函数最为神奇的理论推导的地方（公式太难用latex打出来了，这里我就放一张图片）：

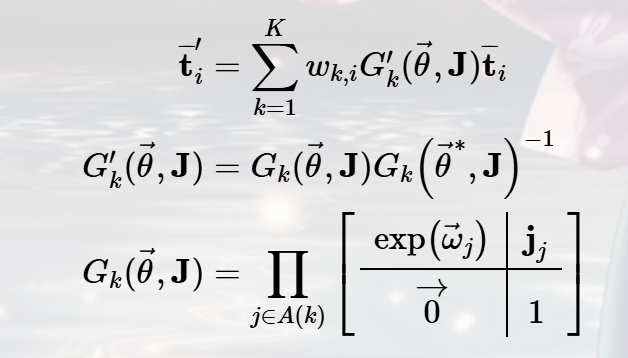
其中，ω_k, i是混合权重矩阵W的元素，代表第k部分的旋转角度有多少程度影响了第i个顶点。

$exp(\vecθ_j)$为局部3 × 3旋转矩阵，对应结点j。

$G_k(\vecθ,J)$ 是关节k的世界变换

$G^′_k(\vecθ,J)$是移除了变换后的相同变换，相当于是在确定你的坐标系

J:关节回归函数。

我们假设W是稀疏的，最多允许四个部分影响一个顶点，那这样子我们对我们的公式还可以进行一定的补充： $$ M(\vecβ,\vecθ;Φ)=W(T_P(\vecβ,\vecθ),J(\vecβ),\vecθ,W)\\ T_p(\vecβ,\vecθ)=\overline T+B_s(\vecβ)+B_p(\vecθ) $$ $B_S(\vecβ),B_P(\vecθ)$表示由shape和pose引起的相对于SMPL标准模板的顶点向量$\overline t_i$的偏移量 $$ \overline t'_i=\sum_{k=1}^{K}w_{k,i}G^′_k(\vecθ,J(\vec\beta))(\overline t_i+b_{s,i}(\vec\beta)+b_{P,i}(\vec\theta)) $$ 其中，$b_{S,i}(\vecβ),b_{P,i}(\vecθ) 分别B_S(\vecβ),B_P(\vec θ)$的顶点，表示相对于顶点$\overline t_i$的偏移量。 $$ B_S(\vecβ;S)=\sum^\vec{|β|}_{n=1}β_nS_n $$

$\vecβ=[β_1,…,β_{|\vecβ|}]^T，|\vecβ|$是线性形状系数的数量。

S_n ∈ R^3N：形状位移的标准正交主分量

$S=[S_1,…,S_{|\vecβ|}]∈R^{3N×|\vecβ|}$为形状位移矩阵。线性函数$B_S(\vecβ;S)$能够完全被矩阵S定义,通过注册训练网络学习。

定义R：$R^{|\vecθ|}↦R^{9K}$为把一个位姿向量映射到连接部分相对旋转矩阵的向量上θ⃗,由于我们的骨骼节点有23个关节，则$R(\vecθ)$是一个23 × 9 = 207维的向量。它的元素是关节旋转角的sin和cos函数，因此它是一个对于θ⃗的非线性函数。

但是作者又定义了一个可以让pose blend shape线性的函数：$R^∗(\vecθ)=(R(\vecθ)−R(\vecθ^∗))$,其中，→θ∗定义了rest pose. 定义$R_n(\vecθ)$为$R(\vecθ)$的第n个向量，则与静止模板的偏差为： $$ B_p(\vec \theta;P)=\sum^{9K}_{n=1}(R_n(\vec \theta)-R_n(\vec\theta^*))P_n $$ 其中，P_n ∈ R^3N表示顶点偏移的向量。

P = [P₁, …, P_9K] ∈ R^3N × 9K是所有207个pose blend shape组成的矩阵。$B_P(\vecθ)$完全被矩阵P定义。

不同的体型有不同的关节位置，每个关节由其在静止位姿（rest pose）中的3D位置表示。关节3D位置相对于身体形状的函数如下： $$ J(\vecβ;J,\overline T,S)=J(\overline T+B_S(\vecβ;S)) $$ 其中，J是将rest vertices转换成rest joints的矩阵，我们从不同的人在不同的姿势的例子中学习回归矩阵J。

SMPL最后被定义为： $$ M(\vecβ,\vecθ;Φ)=W(T_P(\vecβ,\vecθ;\overline T,S,P),J(\vecβ;J,\overline T,S),\vecθ,W) $$ 每个顶点变为： $$ t_i’=\sum_{k=1}^Kw_{k,i}G'_k(\vec\theta,J(\vec\beta;J,\overline T,S))t_{P,i}(\vec\beta,\vec\theta;\overline T,S,P) $$ 其中 $$ t_{P,i}(\vec\beta,\vec\theta;\overline T,S,P)=\overline t_i+\sum_{m=1}^{|\vec\beta|}\beta_ms_{m,i}+\sum^{9K}_{n=1}(R_n(\vec \theta)-R_n(\vec\theta^*))p_{n,i} $$ 理论推导到这边就基本上完整了

实现代码

import numpy as np

class SMPL:
    def __init__(self, model_path):
        # 加载模型参数
        params = np.load(model_path)
        self.v_template = params['v_template']  # 模板网格
        self.shapedirs = params['shapedirs']    # 形状主成分
        self.posedirs = params['posedirs']      # 姿态主成分
        self.J_regressor = params['J_regressor'] # 关节回归器
        self.weights = params['weights']        # 蒙皮权重
        self.kintree_table = params['kintree_table'] # 骨骼树结构
    
    def __call__(self, beta, theta, get_skin=False):
        # 计算形状变形
        v_shaped = self.v_template + np.dot(self.shapedirs, beta)
        
        # 计算关节位置
        J = np.dot(self.J_regressor, v_shaped)
        
        # 计算姿态旋转矩阵
        Rs = self.rodrigues(theta[3:].reshape((-1, 3)))
        pose_feature = (Rs - np.eye(3)).ravel()
        
        # 计算姿态变形
        v_posed = v_shaped + np.dot(self.posedirs, pose_feature)
        
        # 构建全局变换矩阵
        G = self.with_zeros(np.hstack((Rs, J.reshape(-1, 3, 1))))
        parent = {i: self.kintree_table[0, i] for i in range(1, self.kintree_table.shape[1])}
        for i in range(1, G.shape[0]):
            G[i] = np.dot(G[i], np.linalg.inv(G[parent[i]]))
        
        # 蒙皮过程
        T = np.tensordot(self.weights, G, axes=[[1], [0]])
        rest_shape_h = np.hstack((v_posed, np.ones((v_posed.shape[0], 1))))
        v = np.sum(T * rest_shape_h.reshape(-1, 1, 4), axis=2)[:, :3]
        
        return (v, J) if get_skin else J
    
    def rodrigues(self, r):
        # 罗德里格斯公式：将旋转向量转换为旋转矩阵
        theta = np.linalg.norm(r, axis=1).reshape(-1, 1, 1)
        r = r / (theta + 1e-8)
        r = r.reshape(-1, 3)
        cost = np.cos(theta)
        sint = np.sin(theta)
        rx = np.array([[0, -r[:, 2], r[:, 1]],
                       [r[:, 2], 0, -r[:, 0]],
                       [-r[:, 1], r[:, 0], 0]]).transpose(2, 0, 1)
        R = np.eye(3) + sint * rx + (1 - cost) * np.matmul(rx, rx)
        return R
    
    def with_zeros(self, x):
        # 在变换矩阵底部添加一行 [0, 0, 0, 1]
        return np.vstack((x, np.array([[0.0, 0.0, 0.0, 1.0]])))

有了上面的推导，代码基本上就是所见即所得，上面也有一些注释，很好理解

SMPL系列

#SMPL #PxMAF-X #3D人体模型恢复

PxMAF-X学习

http://example.com/2025/07/08/PxMAF-X学习/

作者

牧丛

发布于

2025年7月8日

许可协议

深度学习笔记1 上一篇

线性表整理下一篇